Simulation of Light-Tissue Interaction in Biological Media
| Leitung: | M. Wollweber, B. Roth |
| Team: | O. Melchert |
| Jahr: | 2016 |
Our research activities in subproject 1 of HYMNOS are focused on various numerical aspects of optoacoustics (OAs) in the context of computational biophotonics. Our aim is to perform numerical experiments and to devise measurement protocols that facilitate a better understanding of the features of OA signals that resulting from melanin enriched absorbing structures within tissue. In summary, optoacoustics is a two-part phenomenon consisting of
Part I: Optical absorption of laser beams inducing photothermal heating of tissue
Part II: Acoustic emission of ultrasound waves due to thermoelastic expansion and stress field relaxation
Note that upon irradiation, tissue layers with higher concentration of melanin absorb a greater amount of photothermal energy and expand more intensely than surrounding layers with lower concentration. Whereas the optical absorption is assumed to occur instantaneously, the acoustic propagation of sound waves is a comparatively slow process that occurs on a microsecond timescale. In this regard, note that typical propagation distances are on the order of cm and that the propagation of acoustic waves in soft tissue (i.e. elastic solids) occurs with a speed of v=1400-1600 m/s. Hence, in subproject 1 the challenge is to combine the absorption of laser light by tissue and the acoustic propagation as a multitimescale problem. Our research activity is centered arround three main topics:
Topic 1: The direct OA problem (collaboration of projects HYMNOS and MeDiOO)
One milestone achievement of TP1 features the collaboration of the projects HYMNOS and MeDiOO at HOT in order to complement optoacoustic signals detected in the lab by means of numerical simulations. This collaboration is ultimately aimed at predicting and understanding optoaocustic signal generation in biological tissue.
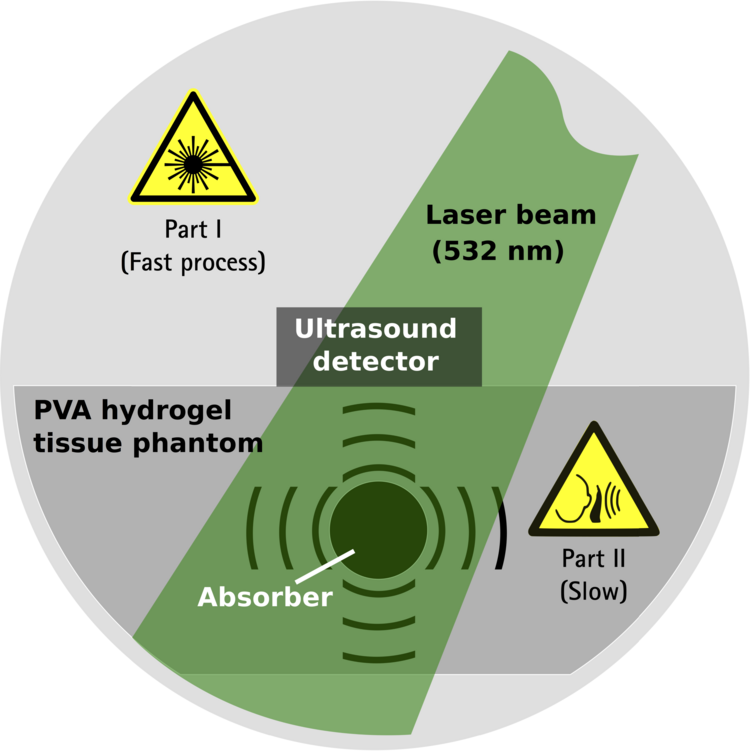
One facet of this collaboration is to shed (laser) light on the principal features of OA signals resulting from measurements on melanin enriched absorbing structures within tissue and to numerically verify OA signals generated in mulit-layered PVA hydrogel phantoms with focus on (nondestructive) OA depth profiling, see Fig. 1 and Ref [E. Blumenroether, O. Melchert, M. Wollweber, B. Roth; Photoacoustics 4 (2016) 125].
We apply the numerical procedure developed in HYMNOS TP1 to model signals observed in the acoustic near- and farfield in both, forward and backward detection mode, in PVA hydrogel tissue phantoms (measurements provided by project MeDiOO), see Fig. 2. Further, for benchmarking, we replicated several laboratory experiments on liquid dye solution reported in the literature. So as to not depend on such validation testing alone, we implemented also more rigorous tests based on effectively one-dimensional limiting cases, to which we compare our fully 3D simulations, see Ref. [O. Melchert, E. Blumenroether, M. Wollweber, B. Roth; arXiv:1702.07603].
Recently, we created a software tool that implements a simple electromechanical finite difference model to study the response of a piezoelectric polyvinylidenflourid (PVDF) transducer to trespassing OA pressure waves in the acoustic nearfield prior to thermal relaxation of the OA source volume. Complementing transducer signals measured in a controlled laboratory experiment with numerical simulations that result from a model of the experimental setup, we find that, bearing in mind the apparent limitations of the one-dimensional approach, the simulated transducer signals can be used very well to predict and interpret the experimental findings, see Fig. 3 and Ref. [O. Melchert, E. Blumenroether, M. Wollweber, B. Roth; tba].
Topic 2: The inverse OA problem
Here, our aim is to solve the OA source reconstruction problem in order to invert OA signals to inintial stress profiles and to infer the optical properties of the underlying material. Therefore we consider the OA problem in the paraxial approximation where the source reconstruction is achieved by the inverse solution of a Volterra integral equation of the second kind, e.g. in terms of a Picard-Lindeloeff iteration scheme, see Fig. 4.
Topic 3: Algorithms in computational biophotonics
Here, we study efficient algorithms for the accurate forward and reverse evaluation of the discrete Fourier-Bessel transform. The transform is used as a numerical tool facilitating a polar convolution of two radially symmetric functions. This is relevant for applications in tissue optics and optoacoustics where a recurrent task is to perform a beam-shape convolution in order to yield the material response to an extended laser beam from its Greens-function response, see Fig.5. The latter results from a more complex measurement process modeled in terms of a Monte Carlo approach and is, in the worst case, known on a finite sequence of coordinate values, only. The considered applications require the repeated (hundreds of times) calculation of a forward and reverse Fourier-Bessel transform. Thus, time-efficiency is key and fast numerical procedures are valuable.
